Bôcher's theorem

In mathematics, Bôcher's theorem can refer to one of two theorems proved by the American mathematician Maxime Bôcher.

Bôcher's theorem in complex analysis

In complex analysis, the theorem states that the finite zeros of the derivative 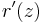r'(z) of a nonconstant rational function 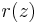r(z) that are not multiple zeros are also the positions of equilibrium in the field of force due to particles of positive mass at the zeros of 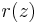r(z) and particles of negative mass at the poles of 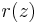r(z) , with masses numerically equal to the respective multiplicities, where each particle repels with a force equal to the mass times the inverse distance.

Bôcher's theorem for harmonic functions

In harmonic analysis, Bôcher's theorem states that a harmonic function in punctured domain (an open domain minus one point in the interior) is a linear combination of a harmonic function in the unpunctured domain with a scaled fundamental solution for the Laplacian in that domain.